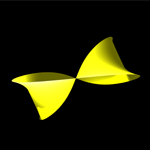
Minimal Surfaces: Helicoid
Example of a Convex Optimization Problem
Drag mouse to rotate model. Hold shift key or use mouse wheel to zoom it.
Given a domain in R2 and an embedding of its boundary in R3, the minimal surface problem is to find an embedding of the entire surface into R3 that is consistent with the boundary embedding and has minimual surface area. This problem is a convex optimization problem. To see the AMPL file that was used to generate the surface shown at right, click here.
LOQO was used to compute the minimal surface shown at right. To get a better feel for the surface, set it in motion by dragging and releasing the object.
Here are some other interesting minimal surfaces: