Roots of Littlewood Polynomials

Roots of Functions: \( \quad F(z) = \displaystyle \sum_{j = 0}^n \alpha_j \; f_j(z) \) where \( \alpha_j \in \{ -1, +1 \} \)

Scroll Down For Some Screen Shots

Click here to see/compute zeros of random polynomials.

\( f_j(z) \) = , n = , \( \alpha_i \)'s =

Size = x center = y center =

Renormalize intensity for real and complex roots together?

This app computes and plots all roots of functions of the form

\( F(z) = \displaystyle \sum_{j = 0}^n \alpha_j \; f_j(z) \)

for which all the coefficients \( \alpha_j \)'s are either \(+1\) or \(-1\) and the functions \( f_j(z) \) are arbitrary analytic functions on the complex plane. The functions \( f_j(z) \) can be selected using the pull-down menu above. The default choice of \( f_j(z) = z^j \) gives us \(n\)-th degree polynomials. The number of terms, \(n\), can also be changed.

Here's a comparison of the location of roots vs critical points: https://vanderbei.princeton.edu/WebGL/roots_critical_points.html

Here's a comparison of the location of roots of a polynomial and all of its derivatives: https://vanderbei.princeton.edu/WebGL/roots_hyper2critical_points.html

Here's my Matlab version of the code: https://vanderbei.princeton.edu/WebGL/PlusMinusOne.m

Here's a related webpage by Dan Christensen: https://jdc.math.uwo.ca/roots/
Here's a related webpage by John Baez: https://math.ucr.edu/home/baez/roots/

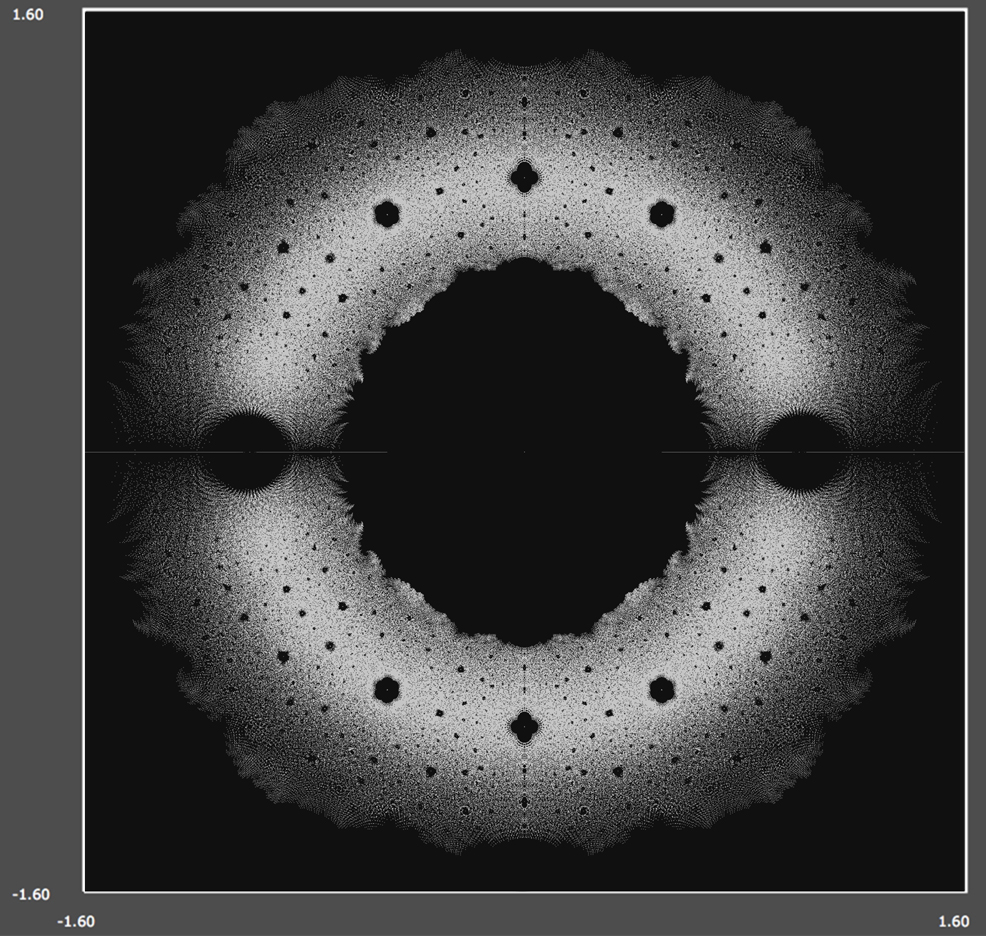
Here's a screenshot for the \(18\)-degree polynomial case...

Here's a screenshot for a closeup view of the \(18\)-degree polynomial case...

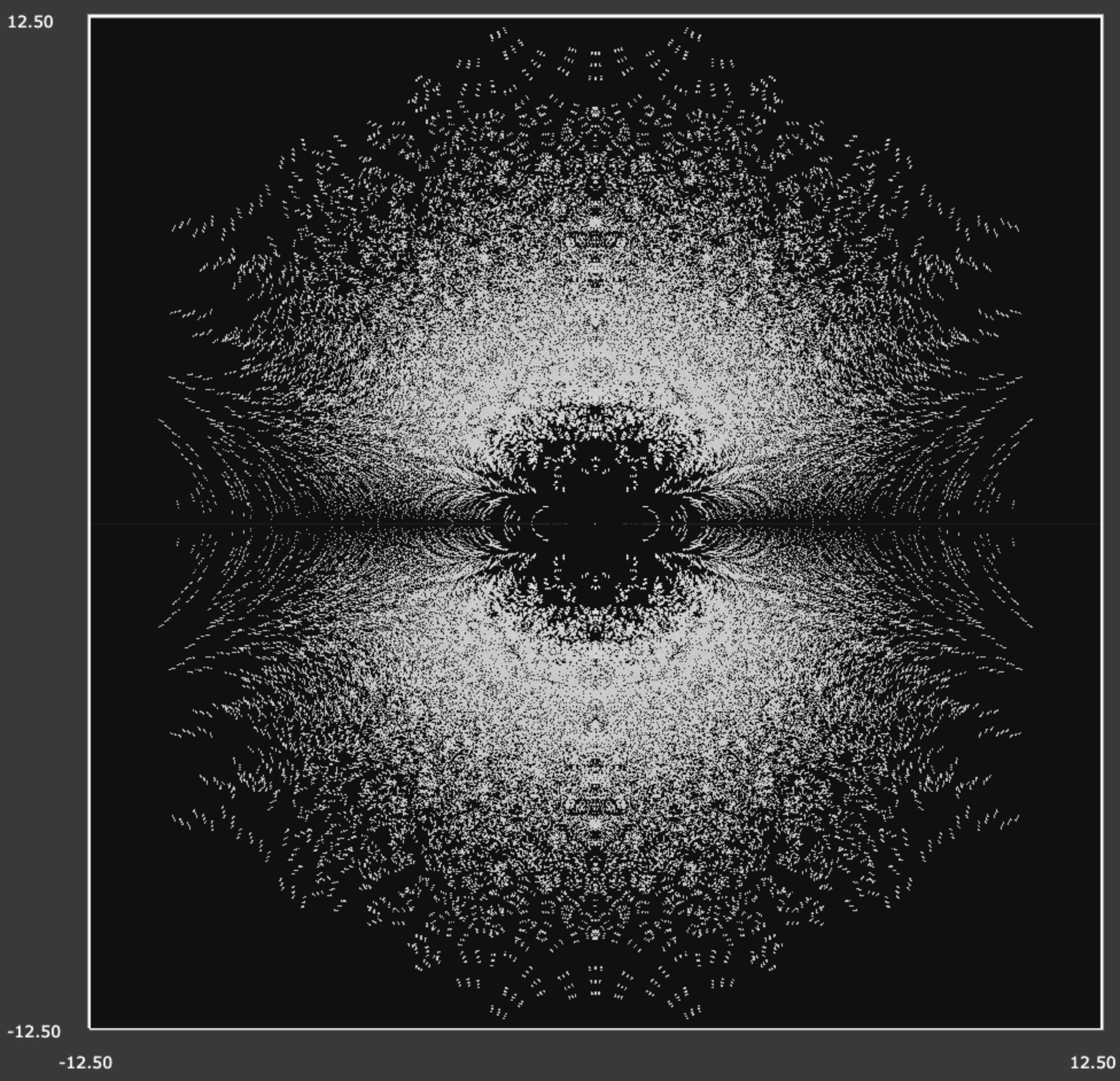
Here's a screenshot for a closeup view of the \(16\)-degree polynomial case...

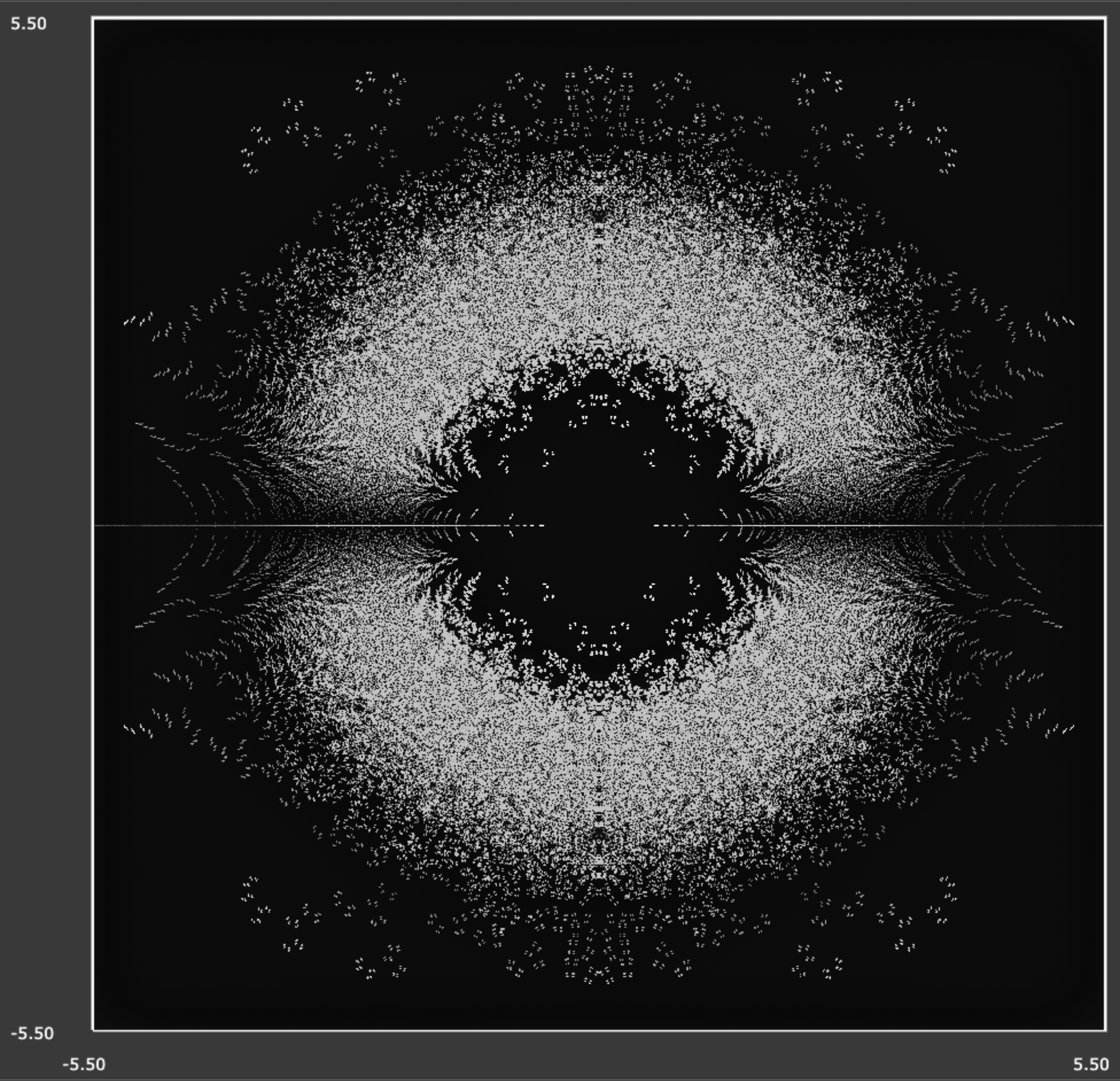
Here's a screenshot for the \(12\)-degree polynomial case with +1,0,-1 coefficients...

Here's a screenshot for a closeup view of the \(12\)-degree polynomial case with +1,0,-1 coefficients...

Here's a screenshot for the \(10\)-degree Taylor polynomial case with +1,0,-1 coefficients...

Here's a screenshot for the \(15\)-degree Sqrt-Taylor polynomial case...

Here's a screenshot for the \(15\)-degree Chebyshev 2nd kind polynomial case...

Updated 2022 Oct 23