Roots of Polynomials

If the Java applet fails to start due to Java Security issues, click here.
Alternatively, you can try this pure Javascript version: Click Here.

This applet computes the complex roots of a large number of randomly generated polynomials and plots them in the complex plane.

By default, the coefficients on the random polynomials are independent Gaussian random variables with mean zero and variance one. Other distributions can be selected from the pull-down menus.

The theoretical density, as derived in this paper, is also shown for comparison.

By default, only 1000 random polynomials are generated. Changing the value to a larger setting, say a few thousand, makes the computation take longer but the empirical distribution begins to look very much like the theoretical density.

Using Matlab, one can compute the empirical distributions much more quickly.
Here's a Matlab code to do it: findroots.m

Here's a few screenshots...

Gaussian:   50 million polynomials:

\( a_0 + a_1 z + \cdots + a_{10} z^{10}, \qquad a_i \in N(0,1) \)


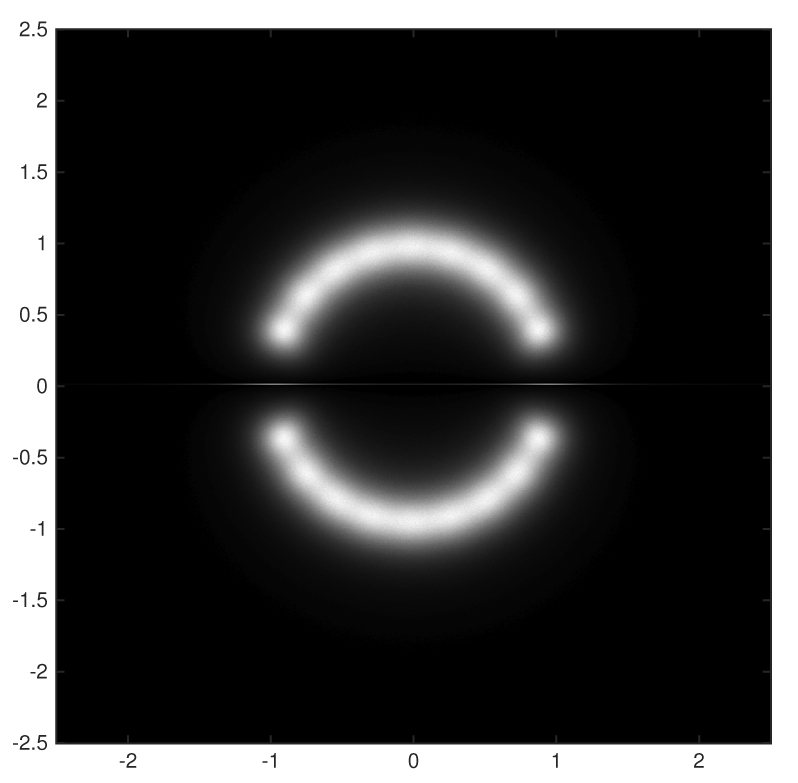Gaussian 50 million

Cauchy:   50 million polynomials:

\( a_0 + a_1 z + \cdots + a_{10} z^{10}, \qquad a_i \in \mbox{Cauchy}(0,1) \)


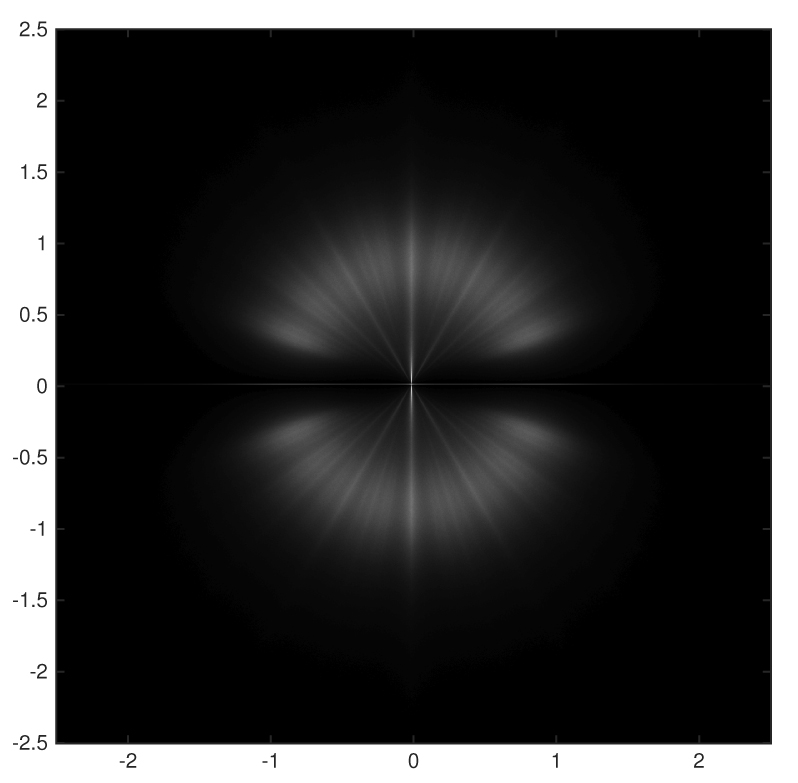Cauchy 50 million
 
 

Taylor Style:   5 million polynomials:

\( a_0 + a_1 z + a_2 \frac{z^2}{2!} + \cdots + a_{10} \frac{z^{10}}{10!}, \qquad a_i \in N(0,1) \)


Gaussian 2 million

Uniform:   500,000 polynomials:

\( a_0 + a_1 z + \cdots + a_{10} z^{10}, \qquad a_i \in \mbox{Unif}(0,1) \)


Cauchy 2 million
 
 

Taylor Style w/ complex coefficients:   5 million polynomials:

\( a_0 + a_1 z + a_2 \frac{z^2}{2!} + \cdots + a_{10} \frac{z^{10}}{10!}, \qquad a_i \in N(0,1) + i N(0,1) \)


Gaussian 2 million

Root Taylor Style w/ complex coefficients:   5 million polynomials:

\( a_0 + a_1 z + a_2 \frac{z^2}{\sqrt{2!}} + \cdots + a_{10} \frac{z^{10}}{\sqrt{10!}}, \qquad a_i \in N(0,1) + i N(0,1) \)


Cauchy 2 million